알고리즘 풀이를 놓은 지 시간이 좀 흐르니까 자신만만하던 문제들도 쉽게 풀지 못하는 지경에 이르렀다. 아무래도 정리를 하면서 이해를 하는 시간을 한 번 더 가져야 할 것 같아서 문제 풀이에 기본이 되는 알고리즘들을 다시 코드를 작성하면서 복기해보려고 한다.
자 가장 쉬운 그래프 탐색법인 DFS부터 알아보자
수많은 트리, 그래프를 순회하는 방법 중 기본이 되는 알고리즘이다.
DFS (Depth First Search)?
이름부터 깊이를 우선하여 서치한다는 의미를 담고 있다. 시작부터 끝까지 '깊이'를 우선하여 탐색한다. 처음에는 깊이를 우선한다는 게 이해가 잘 되지 않을 수 있다. 쉽게 이해하기 위해 미로를 탐험한다고 가정해보자. 무수히 많은 갈림길이 존재할 것이다. 이런 미로를 모두 정복하기 위해 한 방향으로 쭉 걷다가 막힌 곳에서 돌아와 가지 않았던 길을 다시 쭉 가는 방법이다. 그러기 위해서는 이미 갔던 길을 기억해둘 필요가 있다. 특징을 간단히 살펴보고 동작 원리에 대해 알아보겠다.
특징과 장단점
- 연결된 모든 노드를 탐색할 수 있다.
- 깊은 노드에 해가 존재할 경우 금방 해를 구해낼 수도 있다.
- 방문 노드를 기억해두어야 한다.
- 논리 구조가 간단하다.
- 해가 없는 경로에 깊게 빠질 수 있다.
- 처음 얻는 해가 최단 경로라는 보장이 없다.
DFS의 동작 원리
자 만약 이렇게 다섯 개의 노드가 있다고 치자. 연결은 양방향 간선으로 그림과 같이 되어 있다. 탐색하는 방법은 여러가지 일 것이다. 왼쪽으로 갔다가 오른쪽으로 가던지, 오른쪽으로 갔다가 왼쪽으로 가던지, 왼쪽 오른쪽 번갈아 가던지, 코드를 작성하는 사람 마음이다. 시작 노드는 두 번째라 하자.
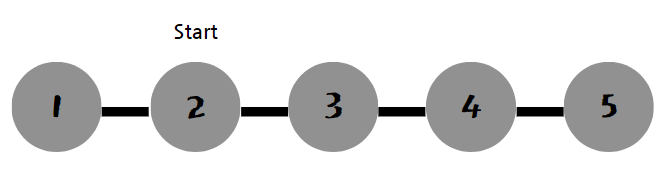
DFS는 이러한 방법들 중 한 길로 쭉 갔다가 하나씩 돌아오는 방식이다. 그걸 알고리즘에서는 깊이 우선이라 한다.
일단 위의 노드에서 우측으로 탐색한다고 가정한다. 왼쪽으로 가는 것도 상관없다. 방문한 곳은 빨감 점으로 표시하겠다.
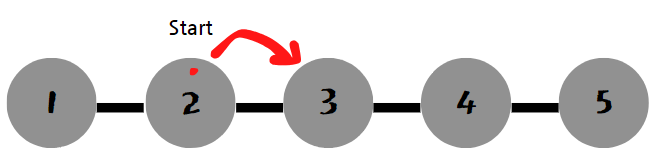
처음으로 3번째 노드를 탐색한다.
그 다음은 4번째 노드를 탐색한다. 3번째 노드에서 갈 수 있는 곳은 4번째 밖에 없기 때문이다.

이렇게 오른쪽 끝에 도달하게 된다면 더 이상 갈 곳이 없다. 이 때는 방금 왔던 길을 그대로 다시 돌아간다.
4번째 노드로 왔을 때도 마찬가지로 이미 3에서 왔고, 5를 갔다 왔기 때문에 뒤로 돌아간다.
이렇게 처음 시작한 2로 돌아오면 이제 가지 않았던 1번 노드를 간다

.

1번 노드도 더 이상 갈 곳이 없기 떄문에 2로 돌아간 뒤, 탐색을 끝낸다.
방문 순서를 나타내면 2 - 3 - 4 - 5 - 1 이다.
이제 코드에 이 탐색법을 녹이기 위해 스택을 도입해서 조금 더 복잡한 트리에서 DFS를 살펴 보겠다.

자 다음과 같은 10개의 노드가 있는 트리를 살펴보겠다. 1번 부터 출발해서 모든 노드를 탐색할 것이다.
스택에는 첫 노드인 1을 저장해준다. 이제 스택에서 하나씩 빼서 갈 수 있는 곳을 스택에 다시 넣어주는 동작을 반복할 것이다. 스택에 남지 않을때까지 말이다.

스택에서 1을 빼온 뒤, 1과 연결된 2와 3을 넣어준다.
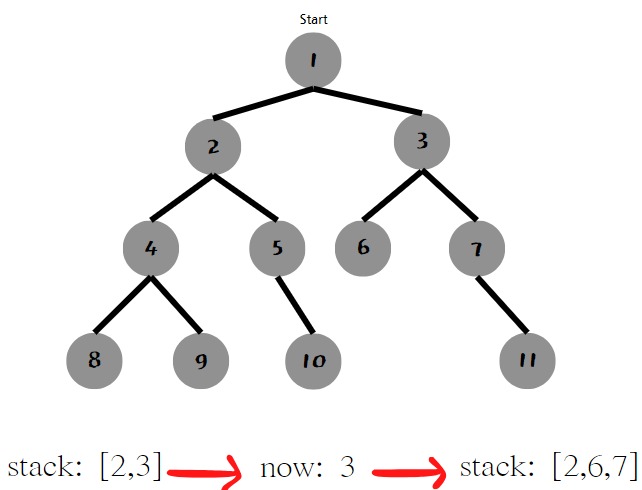
다음으로 [2, 3]에서 3을 빼와 연결된 6, 7 을 넣어준다.
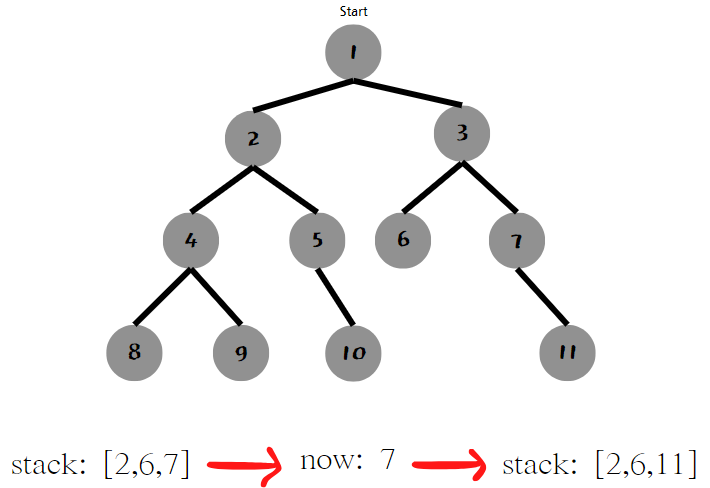
이렇게 한다면 이제 11을 뺄 차례이다. 하지만 11에서는 연결된 곳이 없으므로 앞서 살펴본 것처럼 다시 7로 돌아간다.
7에 연결된 건 11만 있었기 때문에 3까지 돌아간다. 스택에는 3에 연결된 6이 남아있으므로 6을 뺴서 연결된 곳을 살핀다.
이렇게 쭉 탐색하면 이런 순서를 가지게 된다.
1 - 3 - 7 - 11 - 6 - 2 - 5 - 10 - 4 - 9 - 8
이제 스택을 활용한 DFS의 기본적인 탐색 방법을 알았으니 이걸 파이썬 코드로 구현해보겠다.
보통 while 반복문을 통해 구현하고, 재귀로도 구현할 수 있다.
DFS Python 코드1 (while문)
# start는 시작 노드의 번호
# graph는 노드마다 연결된 노드를 저장해 둔 2차원 배열로 가정
## graph[1] = [2, 3], graph[3] = [1, 7]
def dfs(start):
# 방문 배열 vst을 생성한다.
# 첫 노드를 방문했다치고 stack 배열을 만들어 담아준다.
vst = [start]
st = [start]
# stack배열을 비워가며 DFS를 수행한다.
while st:
# stack의 가장 마지막에 있는 노드를 빼온다.
s = st.pop()
# s에 연결된 노드들을 돌면서 방문하지 않은 곳을 방문한다.
for e in graph[s]:
if e not in vst:
vst.append(s)
st.append(e)
return vst
DFS Python 코드2 (재귀)
# graph는 노드마다 연결된 노드를 저장해 둔 2차원 배열로 가정
## graph[1] = [2, 3], graph[3] = [1, 7]
# 방문 배열 vst을 생성한다.
vst = []
def dfs(start):
# 방문 배열에 현재 노드를 담아준다.
vst.append(start)
# start에 연결된 노드들을 돌면서 방문하지 않은 곳을 방문한다.
for e in graph[start]:
if e not in vst:
dfs(e)
dfs[graph, 1]
print(vst)
DFS의 큰 틀은 여기서 벗어나지 않는다. 문제마다 요구하는 답이 다르긴 하지만, 어떤 값을 저장하느냐, 어디에서 값을 더하고 빼주냐, 어디에 어떤 조건을 거느냐 이런 사소한 부분만 바꿔주면 DFS 문제 풀이는 끝이다. DFS로도 안 풀리는 문제가 있다면 그건 DFS로 접근하면 안 되는 문제이다. 노드 순회 문제라고 DFS를 무작정 대입하지 말고 코드 작성 전에 한 번 생각해 보길 바란다.
DFS 기본 문제 풀이 보기
[SWEA] [파이썬 S/W 문제해결 기본] 5일차 - 미로 (python)
https://swexpertacademy.com/main/learn/course/lectureProblemViewer.do SW Expert Academy SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요! swexpertacademy.com 🔥 작성 코드 T = int(input()) for test_cas
dongkeun2.tistory.com
'Algorithm > Algorithm' 카테고리의 다른 글
| [Python] 세그먼트 트리, Segment Tree 구조 이해 (파이썬 코드) (0) | 2024.10.17 |
|---|---|
| [Python] 너비 우선 탐색, BFS (Breadth First Search) 알고리즘 파이썬 코드 (0) | 2024.10.10 |
| [Python] 소수 판별, 소수 리스트 구하기 (feat.에라토스테네스의 체) (0) | 2023.02.03 |
| [Python] 유클리드 호제법 (최대공약수 구하기) (0) | 2023.01.30 |
| 최소 스패닝 트리(MST, Minimum Spanning Tree), Kruskal & Prim 알고리즘 (0) | 2023.01.12 |